Задачи повышенной сложности по математике 10 - 11 класс с решением и ответами.
Задача 1. Найдите все простые числа p и q такие, что p + q = (p – q)³.
Решение:
Ответ: p = 5, q = 3.
Пусть p – q = n, тогда p + q = n³.Отсюда 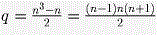 . . Среди трех последовательных целых чисел одно делится на 3, поэтому q делится на 3. Среди простых чисел только 3 делится на 3. Значит, q = 3. Это значение q получается при n = 2. 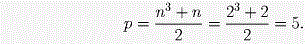
Задача 2. Приведенный квадратный трехчлен f(x) имеет 2 различных корня.
Может ли так оказаться, что уравнение f(f(x)) = 0 имеет 3 различных корня, а уравнение f(f(f(x))) = 0 — 7 различных корней?
Решение:
Ответ: Нет.
Из условия следует, что f(x) = (x – a)(x – b), где a ≠ b.
Пусть искомый многочлен f(x) существует.
Тогда, очевидно f(f(x)) = (x – t1)²(x – t2)(x – t3).
Заметим, что t1, t2, t3 — корни уравнений f(x) = a и f(x) = b, при этом корни этих уравнений не совпадают, поэтому можно считать, что уравнение f(x) = a имеет один корень x = t1.
Рассмотрим уравнение f(f(f(x))) = 0. Его решения, очевидно, являются решениями уравнений f(f(x)) = a и f(f(x)) = b. Но уравнение f(f(x)) = a равносильно уравнению f(x) = t1 и имеет не более двух корней, а уравнение f(f(x)) = b — не более четырех корней (как уравнение четвертой степени).
То есть уравнение f(f(f(x))) = 0 имеет не более 6 корней.
Задача 3. Пусть AD — биссектриса треугольника ABC, и прямая l касается окружностей, описанных около треугольников ADB и ADC в точках M и N соответственно.
Докажите, что окружность, проходящая через середины отрезков BD, DC и MN, касается прямой l.
Решение:
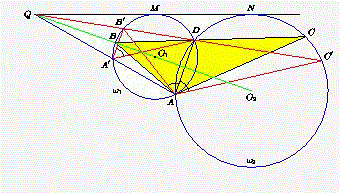
Решение 1.
Обозначим центры окружностей, описанных около треугольников ADB и ADC через O1 и O2, а середины отрезков BD, DC, MN, DO2 и O1O2 — через A1, A2, K, E и O соответственно (см. рис.). Пусть ∠ BAD = ∠ CAD = α . Тогда ∠ A1O1D = ∠ A2O2D = α (так как половина центрального угла равна вписанному, опирающемуся на ту же дугу). Отрезок OK — средняя линия трапеции (или прямоугольника) O1MNO2, следовательно, OK ⊥ l, и 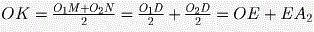 . Заметим, что точки E, O и A2 лежат на одной прямой, так как ∠ OEO2 + ∠ O2EA2 = ∠ O1DO2 + ∠ O2EA2 = ∠ O1AO2 + (180° – ∠ DO2C) = 2 α + (180° – 2 α ) = 180°, т.е. OK = OE + EA2 = OA2. Аналогично доказывается, что OA1 = OK. Значит, точки A1, A2 и K лежат на окружности с центром O, а так как OK ⊥ l, то эта окружность касается прямой l. . Заметим, что точки E, O и A2 лежат на одной прямой, так как ∠ OEO2 + ∠ O2EA2 = ∠ O1DO2 + ∠ O2EA2 = ∠ O1AO2 + (180° – ∠ DO2C) = 2 α + (180° – 2 α ) = 180°, т.е. OK = OE + EA2 = OA2. Аналогично доказывается, что OA1 = OK. Значит, точки A1, A2 и K лежат на окружности с центром O, а так как OK ⊥ l, то эта окружность касается прямой l.Случай, когда вместо прямой l рассматривает-ся прямая l1, разбирается аналогично.
Решение 2.
Пусть радиусы окружностей, описанных около треугольников ADB и ADC равны R1 и R2. Если эти радиусы различны, то прямая l пересекает линию центров O1O2 в точке O (см. рис.). Пусть OD пересекает окружности в точках B′ и C′, и OA пересекает ω в точке A′. При гомотетии H с центром O и коэффициентом 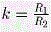 точки C′, D и A переходят в точки D, B′ и A′ соответственно, следовательно, ∠ DAC′ = ∠ B′A′D. С другой стороны, ∠ B′A′D = ∠ B′AD, поэтому ∠ B′AD = ∠ C′AD. А это означает, что точки B′ и C′ совпадают с точками B и C, так как в противном случае один из углов BAD и CAD был бы меньше α , а другой — больше α ( α = ∠ B′AD = ∠ C′AD). точки C′, D и A переходят в точки D, B′ и A′ соответственно, следовательно, ∠ DAC′ = ∠ B′A′D. С другой стороны, ∠ B′A′D = ∠ B′AD, поэтому ∠ B′AD = ∠ C′AD. А это означает, что точки B′ и C′ совпадают с точками B и C, так как в противном случае один из углов BAD и CAD был бы меньше α , а другой — больше α ( α = ∠ B′AD = ∠ C′AD). Рассмотрим гомотетию H1 с центром O, переводящую ω 2 в окружность ω , проходящую через точку E — середину отрезка MN. Из того, что l проходит через точку O и ω 2 касается l, следует, что ω касается l в точке E. Кроме того, из гомотетичности треугольников ONC и OMD (гомотетия H) следует, что NC || MD. Кроме того, H1(C) = C1, где EC1 || NC. Поэтому EC1 — средняя линия трапеции CNMD, т.е. гомотетия H1 переводит точку C в середину DC. Аналогично, она переводит D в середину отрезка BD. Значит, ω проходит через середины отрезков BD и DC. Если же R1 = R2, то вместо гомотетии следует рассмотреть параллельный перенос на вектор 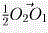 . .
Решение 3.
Пусть R1 ≠ R2. Проведем перпендикуляр SO к плоскости π , содержащей окружности ω 1 и ω 2 (см. обозначения в предыдущем решении). Нетрудно понять, что пересечение (наклонного) конуса с вершиной S и основанием ω 1 и прямого кругового цилиндра с основанием ω 2 является окружность, равная ω 2 и лежащая в плоскости π 1 || π . Глядя на рис., заключаем, что ортогональной проекцией на плоскость π пересечения конуса и плоскости, равноудаленной от π и π 1 является окружность, проходящая через середины отрезков BD, DC и MN и касающаяся прямой MN. В случае R1 = R2 вместо конуса следует рассмотреть (наклонный) цилиндр с основанием ω 1.
Задача 4. Дана последовательность xk такая, что x1 = 1, xn + 1 = n sin xn + 1.
Докажите, что последовательность непериодична.
Решение:
Предположим, что она периодична и длина периода равна T, тогда xm + T = xm и xm + T + 1 = xm + 1 при m ≥ m0.
Если при некотором m ≥ m0 sin xm ≠ 0, то xm + T + 1 = (m + T) sin xm + T + 1 = (m + T) sin xm + 1 ≠ m sin xm + 1 = xm + 1.
А если sin xm = 0, то xm + 1 = 1, и sin xm + 1 = sin 1 ≠ 0, так что предыдущее рассуждение применимо к xm + 1.
Таким образом получаем противоречие.
Задача 5. Докажите, что если у тетраэдра два отрезка, идущие из вершин некоторого ребра, в центры вписанных окружностей противолежащих граней, пересекаются, то отрезки, выпущенные из вершин скрещивающегося с ним ребра в центры вписанных окружностей двух других граней, также пересекаются.
Решение:
Пусть A1 — центр вписанной окружности ∆ SBC, B1 — центр вписанной окружности ∆ SAC, AA1 пересекается с 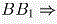 A, A1, B1, B лежат в одной плоскости, значит прямые AB1 и BA1 пересекаются на ребре SC. Пусть точка пересечения этих прямых — p. Так как Ap и Bp — биссектрисы углов A и B, то A, A1, B1, B лежат в одной плоскости, значит прямые AB1 и BA1 пересекаются на ребре SC. Пусть точка пересечения этих прямых — p. Так как Ap и Bp — биссектрисы углов A и B, то 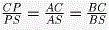 . Но тогда AC • BS = BC • AS, отсюда . Но тогда AC • BS = BC • AS, отсюда 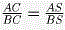 , следовательно биссектрисы углов S в ∆ ASB и C в ∆ ACB пересекаются на ребре AB, т.е. точки S, C и центры вписанных окружностей ∆ ASB и ∆ ACB лежат в одной плоскости. Отсюда следует, что отрезки, соединяющие вершины S и C с центрами вписанных окружностей противолежащих граней, пересекаются. , следовательно биссектрисы углов S в ∆ ASB и C в ∆ ACB пересекаются на ребре AB, т.е. точки S, C и центры вписанных окружностей ∆ ASB и ∆ ACB лежат в одной плоскости. Отсюда следует, что отрезки, соединяющие вершины S и C с центрами вписанных окружностей противолежащих граней, пересекаются.
Задача 6. На плоскости дано бесконечное множество точек S, при этом в любом квадрате 1 × 1 лежит конечное число точек из множества S. Докажите, что найдутся две разные точки A и B из S такие, что для любой другой точки X из S выполняется: |XA|,\;|XB| ≥ 0,999|AB|.
Решение:
Докажем утверждение задачи от противного.
Можно предположить, что для любых двух разных точек A и B из S найдется отличная от них точка X из S такая, что либо XA < 0,999AB, либо XB < 0,999AB.
Переформулируем вышеприведенное утверждение: для любого отрезка I с концами в S и длиной l найдется отрезок I′ с концами в S длины не более 0,999l, один из концов которого совпадает с некоторым концом I.
Или, иначе говоря, I′ пересекает I.
Возьмем теперь первый отрезок I1 длины l и будем брать отрезки I2, I3, …так, что Ik + 1 пересекается с Ik и |Ik + 1| < 0,999|Ik|.
Все эти отрезки имеют концы в S. Ломаная не короче отрезка, соединяющего ее концы, поэтому расстояние от любого конца Ik до любого конца I1 не превосходит 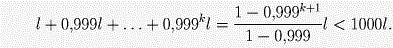
Следовательно, в квадрате 2000l × 2000l с центром в любом из концов I1 лежит бесконечное число точек S.
Но из условия следует конечность их числа в любом квадрате.Полученное противоречие завершает доказательство.
Задача 7. Докажите, что в любом множестве, состоящем из 117 попарно различных трехзначных чисел, можно выбрать 4 попарно непересекающихся подмножества, суммы чисел в которых равны.
Решение:
Лемма.
Из любых 61 различных трехзначных чисел можно выбрать две непересекающиеся пары чисел, суммы в которых равны.
Доказательство:
Из 61 числа можно образовать 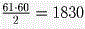 пар чисел, сумма чисел в каждой паре лежит между 200 и 2000, следовательно, у каких-то двух пар суммы совпадают. пар чисел, сумма чисел в каждой паре лежит между 200 и 2000, следовательно, у каких-то двух пар суммы совпадают.
Пары, для которых совпадают суммы, очевидно, не могут пересекаться, ибо если x + y = x + z, то y = z и пары совпадают.
Лемма доказана.
Выберем пару пар чисел с равными суммами 15 раз (каждый раз будем исключать из рассматриваемого набора 4 взятых числа, перед последующим выбором чисел останется как раз 61 число).
Если не все 15 сумм были различны, то мы нашли 4 искомых множества — это 4 пары чисел, у которых совпадают суммы.
Если все 15 сумм различны, то составим два множества пар N1 и N2 таким образом: из двух пар с равными суммами первую включим в N1, вторую — в N2. Рассмотрим первое множество пар. У него есть 215 подмножеств.
Сумма всех чисел во всех парах любого подмножества не превосходит 30,000 тысяч (чисел не больше 30, каждое меньше тысячи).
Но 215 > 30\,000, следовательно, есть два подмножества, для которых суммы чисел, входящих во все их пары совпадают.
Выбросив из этих подмножеств их пересечение, получим непересекающиеся подмножества M1 и M2 с тем же условием.
Теперь в N2 возьмем подмножества пар, соответствовавших парам из множеств M1 и M2 — M3 и M4.
Множества чисел, входящих в пары M1, M2, M3, M4 — искомые.
Комментарий: Из аналогичных соображений выбирая не только пары, но также тройки и четверки, можно показать, что четыре непересекающиеся подмножества с равными суммами можно выбрать среди любых 97 трехзначных чисел.
|

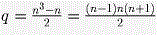 .
.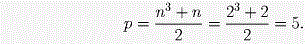

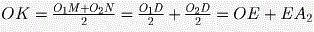 . Заметим, что точки E, O и A2 лежат на одной прямой, так как ∠ OEO2 + ∠ O2EA2 = ∠ O1DO2 + ∠ O2EA2 = ∠ O1AO2 + (180° – ∠ DO2C) = 2 α + (180° – 2 α ) = 180°, т.е. OK = OE + EA2 = OA2. Аналогично доказывается, что OA1 = OK. Значит, точки A1, A2 и K лежат на окружности с центром O, а так как OK ⊥ l, то эта окружность касается прямой l.
. Заметим, что точки E, O и A2 лежат на одной прямой, так как ∠ OEO2 + ∠ O2EA2 = ∠ O1DO2 + ∠ O2EA2 = ∠ O1AO2 + (180° – ∠ DO2C) = 2 α + (180° – 2 α ) = 180°, т.е. OK = OE + EA2 = OA2. Аналогично доказывается, что OA1 = OK. Значит, точки A1, A2 и K лежат на окружности с центром O, а так как OK ⊥ l, то эта окружность касается прямой l.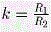 точки C′, D и A переходят в точки D, B′ и A′ соответственно, следовательно, ∠ DAC′ = ∠ B′A′D. С другой стороны, ∠ B′A′D = ∠ B′AD, поэтому ∠ B′AD = ∠ C′AD. А это означает, что точки B′ и C′ совпадают с точками B и C, так как в противном случае один из углов BAD и CAD был бы меньше α , а другой — больше α ( α = ∠ B′AD = ∠ C′AD).
точки C′, D и A переходят в точки D, B′ и A′ соответственно, следовательно, ∠ DAC′ = ∠ B′A′D. С другой стороны, ∠ B′A′D = ∠ B′AD, поэтому ∠ B′AD = ∠ C′AD. А это означает, что точки B′ и C′ совпадают с точками B и C, так как в противном случае один из углов BAD и CAD был бы меньше α , а другой — больше α ( α = ∠ B′AD = ∠ C′AD).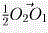 .
.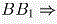 A, A1, B1, B лежат в одной плоскости, значит прямые AB1 и BA1 пересекаются на ребре SC. Пусть точка пересечения этих прямых — p. Так как Ap и Bp — биссектрисы углов A и B, то
A, A1, B1, B лежат в одной плоскости, значит прямые AB1 и BA1 пересекаются на ребре SC. Пусть точка пересечения этих прямых — p. Так как Ap и Bp — биссектрисы углов A и B, то 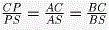 . Но тогда AC • BS = BC • AS, отсюда
. Но тогда AC • BS = BC • AS, отсюда 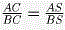 , следовательно биссектрисы углов S в ∆ ASB и C в ∆ ACB пересекаются на ребре AB, т.е. точки S, C и центры вписанных окружностей ∆ ASB и ∆ ACB лежат в одной плоскости. Отсюда следует, что отрезки, соединяющие вершины S и C с центрами вписанных окружностей противолежащих граней, пересекаются.
, следовательно биссектрисы углов S в ∆ ASB и C в ∆ ACB пересекаются на ребре AB, т.е. точки S, C и центры вписанных окружностей ∆ ASB и ∆ ACB лежат в одной плоскости. Отсюда следует, что отрезки, соединяющие вершины S и C с центрами вписанных окружностей противолежащих граней, пересекаются.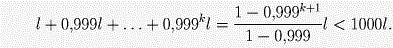
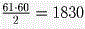 пар чисел, сумма чисел в каждой паре лежит между 200 и 2000, следовательно, у каких-то двух пар суммы совпадают.
пар чисел, сумма чисел в каждой паре лежит между 200 и 2000, следовательно, у каких-то двух пар суммы совпадают.