Олимпиадные задачи по математике 9 класс с решением и ответами.
Олимпиадные задания - задачи олимпиад. Решение. Ответы.
Задача № 1 : Решение задач :
В трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60°.
Докажите, что трапеция – равнобедренная.
Задача № 2 :
Имеются два сосуда, в первом из них 1 л воды, второй сосуд пустой.
Последовательно проводятся переливания из первого сосуда во второй, из второго в первый и т. д.,
причем доля отливаемой воды составляет последовательно 1/2, 1/3, 1/4 и т. д. от количества воды в сосуде,
из которого вода отливается.
Сколько воды будет в сосудах после 2007 переливаний?
Задача № 3 :
Решите неравенство :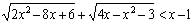 
Задача № 4 :
Решите уравнение : x2 + 2005x – 2006 = 0.
Задача № 5 :
Стрелок десять раз выстрелил по стандартной мишени и выбил 90 очков.
Сколько попаданий было в семерку, восьмерку и девятку,
если десяток было четыре, а других попаданий и промахов не было?
Задача № 1 :
Пусть AD = a, BC = b, AC = a + b. Продолжим AD за точку D на расстояние DM = BC.
Тогда очевидно, что ?АСМ - равносторонний.
Но это значит, что угол АОD и угол ВОС - тоже равносторонние.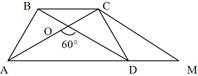
Отсюда непосредственно следует, что угол АОВ = угол СОD,
откуда имеем, что AB = CD.
Задача № 2 :
Просчитав» несколько первых переливаний, нетрудно обнаружить,
что после первого, третьего, пятого переливаний в обоих сосудах будет по ½ л воды.
Необходимо доказать, что так будет после любого переливания с нечетным номером.
Если после переливания с нечетным номером 2k-1 в сосудах было по ½ л,
то при следующем переливании из второго сосуда берется 1/(2k + 1) часть,
так что в первом сосуде оказывается - 1/2 + (2/ 2(2k + 1)) = (k + 1)/(2k + 1) (л).
При следующем переливании, имеющем номер 2k+1, из него берется 1/(2k + 2) часть и остается
(k + 1)/(2k + 1)-(k + 1)/((2k + 1)(2k + 1)) = 1/2 (л).
Поэтому после седьмого, девятого и вообще любого нечетного переливания в сосудах будет по ½ л воды.
Задача № 3 :
Заметим, что все решения исходного неравенства существуют, если подкоренные выражения неотрицательны. Одновременно эти неравенства выполняются лишь при условии x2 – 4x + 3 = 0. Это уравнение имеет два корня 1 и 3. Проверка показывает, что исходное неравенство имеет единственное решение 3.
Задача № 4 :
Исходное уравнение имеет очевидный корень 1.
Второй корень найдем по формулам Виета. Так как x1x2 = -2006 и x1 = 1, то x2 = 2006.
Задача № 5 :
Так как стрелок попадал лишь в семерку, восьмерку и девятку в остальные шесть выстрелов,
то за три выстрела (по одному разу в семерку, восьмерку и девятку) он наберет 24 очка.
Тогда за оставшиеся 3 выстрела надо набрать 26 очков. Что возможно при единственной комбинации 8 + 9 + 9 = 26.
Итак, в семерку стрелок попал 1 раз, в восьмерку – 2 раза, в девятку – 3 раза.