Олимпиада по математике 10 класс
Добиться хороших результатов в олимпиадах можно только путем прорешивания как можно большего количества задач.
Варианты олимпиад по математике 10 класс с ответами и решением :
1 вариант | 2 вариант | 3 вариант
Решение задач олимпиад по математике
Задача
Две окружности O и O1 пересекаются в точке A .
Провести через точку A такую прямую,
чтобы отрезок BC , высекаемый на ней окружностями O и O1 , был равен данному.
Решение
Пусть задача решена.
Отрезок BC прямой, проходящей через точку пересечения двух окружностей A , равен данному отрезку a .
Опустим из центров окружностей O и O1 перпендикуляры OE и O1F на эту прямую.
Из центра O1 проведем прямую O1K , параллельную EF (смотри рисунок). EFO1K – прямоугольник, KO1=EF, EF=EA+AF, BE=EA, AF=FC , так как хорды делятся перпендикулярными к ним радиусами пополам. Поэтому EF=BE+FC=a/2 .
Построение сводится к построению прямоугольного треугольника KOO1 по гипотенузе OO1 и катету KO1=EF=a/2 .
Построив этот треугольник, проводим искомую прямую параллельно O1K через точку A или опускаем из точки A перпендикуляр на OK .
Поскольку по одну сторону от данного отрезка OO1 можно построить два равных симметричных прямоугольных треугольника, то задача имеет два решения.
Два решения будет и в том случае, когда получится только один равнобедренный треугольник, так как в этом случае его катеты равноправны и условию задачи будет удовлетворять перпендикуляр, опущенный на каждый из катетов.
Построение возможно, если возможно построение прямоугольного треугольника, т. е. если a/2 < OO1 .
В случае a/2 = OO1 решение также возможно, но оно будет единственным.
Это будет прямая, проходящая через точку А параллельно линии центров.
Задача № 1 :
Назовем "соросовским произведением" двух различных чисел, a и b, число a + b + ab.
Можно ли, исходя из чисел 1 и 4,
после многократного применения этой операции к уже полученным произведениям получить:
а) число 1999;
б) число 2000?
Задача № 2 :
На валютной бирже продаются динары (D), гульдены (G), реалы (R) и талеры (T).
Биржевые игроки имеют право совершать сделку купли-продажи с каждой парой валют не более одного раза в день.
Курсы обмена следующие: D = 6G; D = 25R; D = 120T; G = 4R; G = 21T; R = 5T. Утром у игрока имелось 32 динара.
Какое максимальное число
а) динаров;
б) талеров
он может получить к вечеру?
Задача № 3 :
Центр окружности, проходящей через середины всех сторон треугольника АВС, лежит на биссектрисе его угла С. Найдите сторону АВ, если ВС = а, АС = b(a не равно b).
Задача № 4 :
Решите уравнение
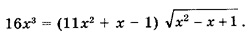
Задача № 5 :
Известно, что существует прямая,
делящая периметр и площадь некоторого описанного около окружности многоугольника в одном и том же отношении.
Докажите, что эта прямая проходит через центр указанной окружности.
Задача № 6 :
Пусть a3 – a– 1 = 0. Найдите точное значение выражения
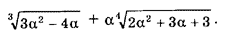
Задача № 7 :
Пусть прямая, перпендикулярная стороне AD параллелограмма ABCD, проходящая через точку В,
пересекает прямую CD в точке M, а прямая, проходящая через точку В и перпендикулярная стороне CD,
пересекает прямую AD в точке N.
Докажите, что прямая, проходящая через точку В перпендикулярно диагонали АС,
проходит через середину отрезка MN.
Задача № 8 :
Возьмем на стороне ВС треугольника АВС произвольную точку D
и проведем окружность через точку D и центры окружностей, вписанных в треугольники ABD и АCD.
Докажите, что все окружности, полученные для различных точек D стороны ВС, имеют общую точку.