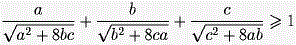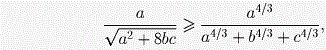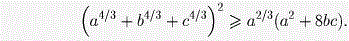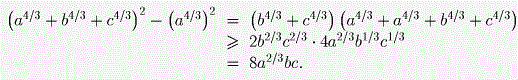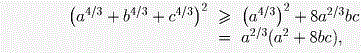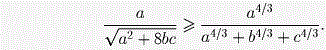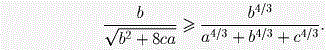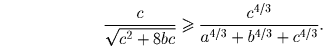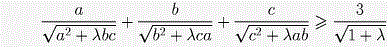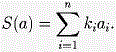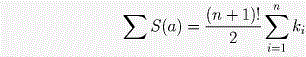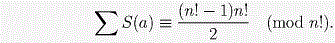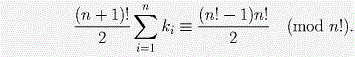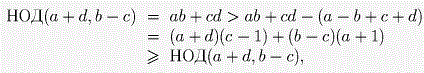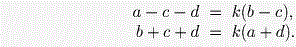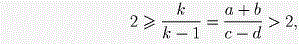Задача 1.
Пусть O – центр описанной окружности остроугольного треугольника ABC, Ap – высота.
Докажите, что если ∠ BCA ≥ ∠ ABC + 30, то ∠ CAB + ∠ COp < 90.
Решение:
Решение 1.
Пусть α = ∠ CAB, β = ∠ ABC, γ = ∠ BCA и δ = ∠ COp.
Пусть точки K и p симметричны точкам A и p соответственно относительно серединного перпендикуляра к отрезку BC. Обозначим через R радиус описанной окружности ∆ ABC.
Тогда OA = OB = OC = OK = R. Кроме того, Qp = KA, поскольку KQpA – прямоугольник.
Теперь заметим, что ∠ AOK = ∠ AOB – ∠ KOB = ∠ AOB – ∠ AOC = 2 γ – 2 β ≥ 60 и, учитывая, что OA = OK = R, получим KA ≥ R и Qp ≥ R.
По неравенству треугольника Op + R = OQ + OC > QC = Qp + pC ≥ R + pC.
Отсюда следует, что Op > pC и, значит, в ∆ COp ∠ pOC > δ . Поскольку α = ½ ∠ BOC = ½(180 – 2 ∠ pCO), то действительно ∠ α + ∠ δ < 90. 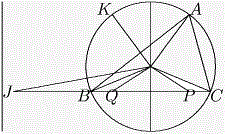
Решение 2
Как и в предыдущем решении, достаточно показать, что Op > pC.
Вспомним, что по теореме синусов AB = 2R sin γ и AC = 2R sin β .
Отсюда получаем: Bp – pC = AB cos β – AC cos γ = 2R( sin γ cos β – sin β cos γ ) = 2R sin ( γ – β ). Учитывая, что 30 ≤ γ – β < γ < 90, видим, что Bp – pC ≥ R.
Значит R + Op = BO + Op > Bp ≥ R + pC, откуда Op > OC, что и требовалось.
Решение 3
Сначала докажем, что R² > Cp • CB. Для этого, поскольку CB = 2R sin α и Cp = AC cos γ , достаточно показать, что ¼ > sin α sin β cos γ .
Заметим, что 1 > sin α = sin ( γ + β ) = sin γ cos β + sin β cos γ и ½ ≤ sin ( γ – β ) = sin γ cos β – sin β cos γ , поскольку 30 ≤ γ – β < 90.
Отсюда следует, что ¼ > sin β cos γ и ¼ > sin α sin β cos γ .
Теперь отметим точку J на BC так, что CJ • Cp = R². Тогда CJ > CB (поскольку R² > Cp • CB), поэтому ∠ OBC > ∠ OJC.
Из того, что OC/CJ = pC/CO и ∠ JOC = ∠ OCp, следует, что ∆ JCO подобен ∆ OCp и ∠ OJC = ∠ pOC = γ .
Значит δ < ∠ OBC = 90 – α , то есть α + δ < 90.
Задача 2. Докажите, что 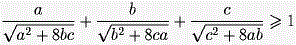
для всех положительных вещественных чисел a, b и c.
Решение:
Сначала докажем, что 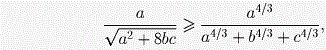
или, что то же самое, 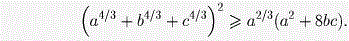
По неравенству о средних 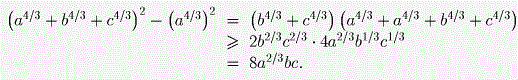
Отсюда 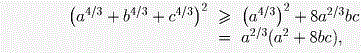
значит 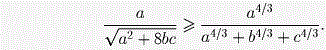
точно также 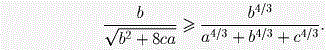
и 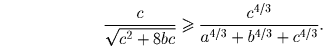
Сложив эти три неравенства, получим: 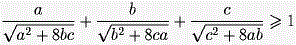
Комментарий. Можно доказать, что для любых a,b,c > 0 и λ ≥ 8 выполняется следующее неравенство: 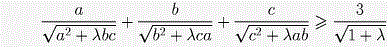
Задача 3. Двадцать одна девочка и двадцать один мальчик принимали участие в математическом конкурсе. - Каждый участник решил не более шести задач.
- Для любых девочки и мальчика найдётся хотя бы одна задача, решённая обоими.
Докажите, что была задача, которую решили не менее трёх девочек и не менее трёх мальчиков.
Решение:
Предположим, что нашлась задача, которую решили не более двух девочек или не более двух мальчиков.
Будем считать задачу «красной», если её решили не более двух девочек и «чёрной» в противоположном случае (тогда её решили не более двух мальчиков).
Представим шахматную доску с 21-й строкой, каждая из которых соответствует девочке, и 21-м столбцом, каждый из которых соответствует мальчику.
Тогда каждая клетка соответствует паре «мальчик–девочка». Каждую клетку покрасим в цвет какой-нибудь задачи, которую решили и мальчик-строка и девочка-столбец.
По принципу Дирихле в каком-нибудь столбце найдётся 11 чёрных клеток, или в какой-нибудь строке найдутся 11 красных клеток (потому что иначе получится, что всего клеток не более чем 21 • 10 + 21 • 10 < 21²).
Рассмотрим, например, девочку-строку, содержащую хотя бы 11 чёрных клеток.
Каждой из этих клеток соответствует задача, решённая максимум двумя мальчиками.
Тогда мы можем указать не менее 6 различных задач, решённых этой девочкой. В силу первого условия никаких других задач девочка не решала, но тогда максимум 12 мальчиков имеют общие решённые задачи с этой девочкой, что противоречит второму условию.
Точно также разбирается случай, если в каком-нибудь столбце найдутся 11 красных клеток.
Задача 4. Пусть N – нечетное натуральное число большее 1, а k1, k2,…kn – произвольные целые числа. Для каждой из n! перестановок a = (a1,a2, … ,an) чисел 1, 2,…n, обозначим 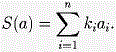
Докажите, что найдутся две такие перестановки b и c (b ≠ c), что n! является делителем S(b) – S(c).
Решение:
Пусть ∑ S(a) – сумма S(a) по всем n! перестановкам a = (a1,a2, … an). Мы вычислим ∑ S(a) двумя способами и достигнем противоречия в случае, если n нечётно.Первый способ. В ∑ S(a) число k1 умножается на каждое i ∈ 1, … ,n всего (n – 1)! раз, по одному на каждую перестановку 1,2, … n, в которой a1 = i. Поэтому коэффициент при k1 в ∑ S(a) равен (n – 1)!(1 + 2 + … + n) = (n + 1)!/2. Это верно для всех ki, поэтому 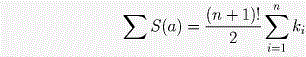
Второй способ. Если n! не является делителем S(b) – S(c) для любого b ≠ c, то все суммы S(a) должны иметь различные остатки при делении на n!.
Поскольку всего перестановок n!, эти остатки в точности равны 0, 1, …, n! – 1.
Поэтому 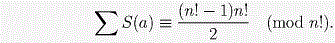
Таким образом 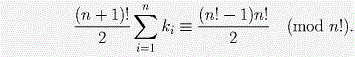
Но для нечётных n левая часть этого сравнения сравнима с 0 по модулю n!, в то время как при n > 1 правая часть не может быть сравнима с 0 (поскольку n! – 1 нечётно).
Мы получили противоречие для всех нечётных n > 1.
Задача 5. В треугольнике ABC проведена биссектрисы Ap и BQ. Известно, что ∠ BAC = 60 и что AB + Bp = AQ + QB. Какими могут быть углы треугольника ABC?
Решение:
Обозначим углы треугольника ABC через α = ∠ A = 60, β = ∠ B и γ = ∠ C. Продолжим сторону AB до точки p′ так, чтобы Bp′ = Bp и построим точку p′ на AQ так, чтобы Ap′ = Ap′. Тогда Bp′p – равнобедренный треугольник с углами при основании равными β /2. Поскольку AQ + Qp′ = AB + Bp′ = AB + Bp = AQ + QB, отсюда следует, что Qp′ = QB. Учитывая, что ∆ Ap′p′ равносторонний, а Ap – биссектриса угла A, получаем, что pp′ = pp′.Докажем, что точки B, p и p′ лежат на одной прямой (а, значит, точка p′ совпадает с точкой C. Предположим, что это не так, то есть ∆ Bpp′ – невырожденный. Тогда ∠ pBQ = ∠ pp′B = ∠ pp′Q = β /2, а ∠ Qp′B = ∠ QBp′. Значит ∠ pp′B = ∠ pBp′, то есть Bp = pp′. Тогда треугольник Bpp′ – равносторонний, но из этого следует, что β /2 = 60, и, значит, α + β = 60 + 120 = 180. Противоречие. Поскольку треугольник BCQ равнобедренный, то 120 – β = γ = β /2, поэтому β = 80 и γ = 40. 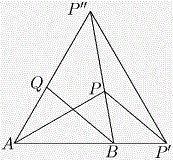
Задача 6. Пусть a, b, c, d – целые числа такие, что a > b > c > d > 0. Предположим, что ac + bd = (b + d + a – c)(b + d – a + c). Докажите, что число ab + cd составное.
Решение:
Предположим, что число ab + cd – простое. Заметим, что ab + cd = (a + d)c + (b – c)a = m • НОД (a + d,b – c) дл некоторого натуральго m. По предположению или m = 1 или НОД (a + d,b – c) = 1. Рассмотрим эти варианты по очереди.1 случай: m = 1. Тогда 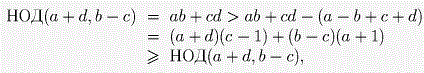
что неверно.2 случай: НОД (a + d,b – c) = 1. Подставляя ac + bd = (a + d)b – (b – c)a в левую часть равенства ac + bd = (b + d + a – c)(b + d – a + c), получаем (a + d)(a – c – d) = (b – c)(b + c + d). Ввиду этого, найдётся такое натуральное число k, что 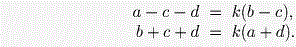
Складывая эти равенства, получаем, что a + b = k(a + b – c + d) и, следовательно, k(c – d) = (k – 1)(a + b). Вспомним, что a > b > c > d. Если k = 1, то c = d – противоречие. Если k ≥ 2, то 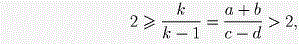
противоречие.В обоих случаях достигнуто противоречие, значит число ab + cd составное.
|