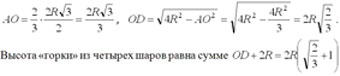Задача № 1 :
Докажите, что уравнение xy = 2006 (x+y) имеет решения в целых числах.
Задача № 2 :
Докажите, что если α, β, γ - углы произвольного треугольника,
то справедливо тождество cos2α + cos2β + cos2γ + 2 cosα cosβ cosγ = 1.
Задача № 3 :
Три шара радиуса R касаются друг друга и плоскости α, четвертый шар радиуса R положен сверху так, что касается каждого из трех данных шаров. Определите высоту «горки» из четырех шаров.
Задача № 4 :
Докажите неравенство x2 - 3x3 < 1/6 на луче [1/4; + ∞).
Задача № 5 :
В прямоугольник 20 x 25 бросают 120 квадратов 1 x 1. Докажите, что в прямоугольник можно поместить круг с диаметром, равным 1, не имеющий общих точек ни с одним из квадратов.
Решение задач :
Задача № 1 :
Преобразуем уравнение к следующему виду: (х – 2006)(у - 2006) = 20062.
Уравнение имеет решения, например, х = у = 4012.
Задача № 2 :
Преобразуем выражение в левой части равенства, учитывая, что α + β + γ = π,
и применяя формулы: cos2x = (1 + cos2x)/2, cosx = - cos(π - x), cosx + cosy = (2cos((x + y)/2))cos((x - y)/2),
получим справедливое тождество.
Задача № 3 :
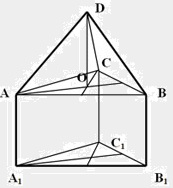
Пусть четыре шара радиуса R c центрами A, B, C, D касаются друг друга и первые три из них – плоскости a в точках A1, B1, C1 (см. рис).
Тогда точки A, B, C, D являются вершинами правильной пирамиды с ребром 2R.
Вершина D этой пирамиды проектируется в центр основания О.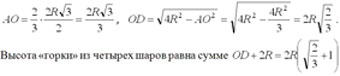
Задача № 4 :
Пусть y = x2 – 3x3. Тогда y' = 2x – 9x2 и с помощью метода интервалов получаем, что y' < 0 при всех x>2/9.
Но 1/4>2/9, следовательно, функция y(x) убывает на луче [1/4; +∞].
Это значит, что x2 - 3x3 < 1/16 - 3/64 = 1/64 < 1/64.
Задача № 5 :
Окружим каждый квадрат полоской шириной 1/2.
Образующие фигуры тоже квадраты со стороной 1 + 2 x 1/2 = 2, имеют площадь равную 4.
Их общая площадь равна 4 x 120 = 480, в то время как искомая площадь равна 500.
Следовательно, найдется точка, которая не покрыта построенными квадратами, но это значит, что она удалена от данных квадратов не меньше чем на по всем направлениям.
Круг радиуса с центром в этой точке не имеет общих точек ни с одним из квадратов.