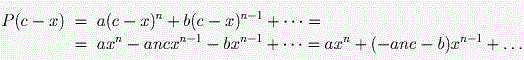Математические задачи 11 класс с решением и ответами.
Задача 1.
О функции f(x), заданной на всей вещественной прямой,
известно, что при любом a > 1 функция f(x) + f(ax) непрерывна на всей прямой.
Докажите, что f(x) также непрерывна на всей прямой.
Решение:
Мы воспользуемся следующими свойствами непрерывных функций: - (1) сумма и разность непрерывных функций — непрерывные функции;
- (2) если g(x) — непрерывная функция, функция g(ax) также непрерывна.
Теперь заметим, что по условию непрерывны функции f(x) + f(2x) и f(x) + f(4x), а в силу свойства (2) вместе с функцией f(x) + f(2x) непрерывна и функция f(2x) + f(4x).
Далее, по свойству (1) непрерывна функция (f(x) + f(2x)) + (f(x) + f(4x)) – (f(2x) + f(4x)) = 2f(x), а, значит, и функция f(x).
Задача 2. В классе каждый ученик — либо болтун, либо молчун,
причем каждый болтун дружит хотя бы с одним молчуном.
Болтун молчит, если в кабинете находится нечётное число его друзей — молчунов.
Докажите, что учитель может пригласить на факультатив не менее половины класса так,
чтобы все присутствующие на факультативе болтуны молчали.
Решение:
Докажем утверждение индукцией по числу n учеников в классе.
Для n = 3 утверждение очевидно.
Предположим, что оно верно при n ≤ N. Пусть n = N + 1.
Утверждение верно, если в классе ровно один молчун. Пусть их не менее двух.
Выделим молчуна A и его друзей — болтунов B1, … ,Bk.
Для оставшихся n – 1 – k учеников утверждение верно, т.е. можно выделить группу M, в которой каждый болтун дружит с нечётным числом молчунов и в M входит не менее 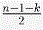 учеников. учеников.
Предположим, что болтуны B1, … ,Bm дружат с нечётным числом молчунов из M, а Bm + 1, … ,Bk — с чётным числом.
Тогда, если 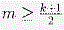 , то добавим к группе M болтунов B1, … ,Bm, , то добавим к группе M болтунов B1, … ,Bm,
а если 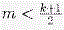 , то добавим к группе M болтунов Bm + 1, … ,Bk и молчуна A. , то добавим к группе M болтунов Bm + 1, … ,Bk и молчуна A.
В обоих случаях мы получим группу учеников, удовлетворяющую условию задачи.
Задача 3. Многогранник описан около сферы.
Назовём его грань большой, если проекция сферы на плоскость грани целиком попадает в грань.
Докажите, что больших граней не больше 6.
Решение:
Пусть R — радиус шара.
Сопоставим каждой большой грани часть граничной сферы шара, расположенную в конусе, вершиной которого служит центр шара, а основанием — проекция шара на эту грань.
Указанная часть сферы является «сферической шапочкой» (то есть частью сферы, лежащей по одну сторону от секущей сферу плоскости) высоты 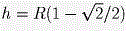 . .
По известной формуле площадь такой «шапочки» равна 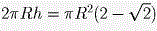 . .
Так как указанные «шапочки» не перекрываются, сумма их площадей не превосходит площади сферы.
Обозначив количество больших граней через n, получим 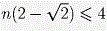 , то есть , то есть 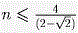 . .
Решение заканчивается проверкой того, что 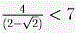 . .
Примечание. Легко видеть, что у куба шесть больших граней.
Поэтому приведенная в задаче оценка числа больших граней является точной.
Задача 4. Существуют ли действительные числа a, b и c такие,
что при всех действительных x и y выполняется неравенство
|x + a| + |x + y + b| + |y + c| > |x| + |x + y| + |y| ?
Решение:
Ответ: Нет.
Предположим, что такие числа a, b и c существуют.
Выберем x > 0 и y > 0 такие, что x + a ≥ 0, x + y + b ≥ 0, y + c ≥ 0.
Тогда разность между левой и правой частями равна a + b + c.
А если взять x < 0 и y < 0 такие, что x + a < 0, x + y + b < 0, y + c < 0,
то эта разность будет равна – a – b – c.
Таким образом, с одной стороны, a + b + c > 0, с другой a + b + c < 0.
Противоречие.
Задача 5. Клетки квадрата 50 × 50 раскрашены в четыре цвета.
Докажите, что существует клетка, с четырех сторон от которой (то есть сверху, снизу, слева и справа)
имеются клетки одного с ней цвета.
Решение:
Предположим, что клетки квадрата n × n удалось раскрасить таким образом, что для любой клетки с какой-то стороны от неё нет клетки одного с ней цвета.
Рассмотрим тогда все клетки одного цвета и в каждой из них нарисуем стрелочку в том из четырёх направлений, в котором клетки того же цвета нет.
Тогда на каждую клетку «каёмки» нашего квадрата будет указывать не более одной стрелки.
Так как клеток каёмки всего 4n – 4, то и клеток каждого цвета не более 4n – 4.
С другой стороны, каждая из n² клеток нашего квадрата раскрашена в один из четырёх цветов, то есть n² ≤ 4(4n – 4).
Для решения задачи теперь достаточно заметить, что последнее неравенство неверно при n = 50.
Несложно убедиться, что оно неверно при всех n ≥ 15, и, следовательно,
утверждение задачи верно уже в квадрате 15 × 15 — а заодно и в любом большем квадрате.
Задача 6. Для бесконечного множества значений многочлена,
существует более одной целой точки, в которой принимаются эти значения.
Докажите, что существует не более одного целого значения многочлена,
принимаемого ровно в одной целой точке.
Решение:
Из условия следует, что многочлен имеет ненулевую степень.
Докажем, что данный многочлен p(x) имеет чётную степень, а его график имеет вертикальную ось симметрии.
Не умаляя общности, мы можем считать старший коэффициент многочлена p(x) положительным
(иначе многочлен можно заменить на – p(x)).
Если p(x) имеет нечётную степень, то при всех достаточно больших по абсолютной величине x он возрастает, и, следовательно, может принимать более чем в одной целой точке лишь конечное число значений.
Поэтому степень p(x) чётна.
Тогда при больших положительных x многочлен возрастает, а при больших по модулю отрицательных x — убывает, и, следовательно, все достаточно большие значения, которые он принимает более чем в одной целой точке, он принимает ровно дважды.
Упорядочим эти значения: a1 < a2 < … — и обозначим xk больший, а yk — меньший прообраз ak.
Таким образом, p(xk) = p(yk) = ak.
Мы докажем, что при достаточно больших k сумма xk + yk постоянна.
Для этого рассмотрим два старших коэффициента p(x): p(x) = axn + bxn – 1 + …
Тогда 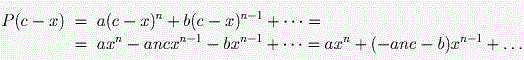
(многоточия скрывают члены не выше (n – 2)-й степени; кроме того, мы воспользовались чётностью n).
Заметим, что коэффициенты при xn у многочленов p(x) и p(c – x) совпадают; что же до коэффициентов при xn – 1, то существует единственное значение c (а именно c0 = – 2b/(an)), при котором совпадают и они.
Если c > c0, то p(x) – p(c – x) — многочлен степени n – 1 с положительным старшим коэффициентом, следовательно, при достаточно больших x его значения положительны.
Поэтому при достаточно больших k xk + yk < c0 + 0.1 (иначе будет p(yk) > p(c0 + 0.1 – xk) > p(xk)). Если, наоборот, c < c0, то p(x) – p(c – x) — многочлен степени n – 1 с отрицательным старшим коэффициентом, значения которого при достаточно больших x отрицательны.
Поэтому при достаточно больших k xk + yk > c0 – 0.1. Но xk + yk — целые числа, поэтому, начиная с некоторого k, все они равны: xk + yk = c. Но тогда многочлены p(x) и p(c – x) совпадают почленно (если не все их коэффициенты совпадают, то при больших x знак p(x) – p(c – x) должен совпадать со знаком первого ненулевого коэффициента этой разности; с другой стороны, среди xk есть сколь угодно большие числа, и для них p(c – xk) = p(yk) = p(xk).)
Итак, p(x) = p(c – x) при всех вещественных x.
Тогда любое значение, принимаемое в целой точке x ≠ c/2, принимается и в точке c – x ≠ x.
Поэтому единственное значение, которое может приниматься ровно в одной целой точке — это p(c/2), да и то, если только c/2 – целое.
|

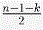 учеников.
учеников.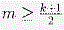 , то добавим к группе M болтунов B1, … ,Bm,
, то добавим к группе M болтунов B1, … ,Bm,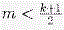 , то добавим к группе M болтунов Bm + 1, … ,Bk и молчуна A.
, то добавим к группе M болтунов Bm + 1, … ,Bk и молчуна A.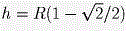 .
.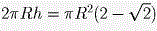 .
.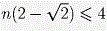 , то есть
, то есть 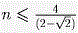 .
.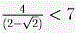 .
.