Школьная олимпиада по математике 11 класс.
1. AD и BE – высоты треугольника АВС.
Оказалось, что точка C', симметричная вершине С относительно середины отрезка DE, лежит на стороне AB.
Докажите, что АВ – касательная к окружности, описанной около треугольника DEC'.
2. Прямая а пересекает плоскость α.
Известно, что в этой плоскости найдутся 2011 прямых,
равноудаленных от а и не пересекающих a. Верно ли, что а перпендикулярна α?
3. Дана неравнобокая трапеция ABCD (AB||CD).
Произвольная окружность, проходящая через точки А и В, пересекает боковые стороны трапеции в точках p и Q, а диагонали – в точках M и N.
Докажите, что прямые pQ, MN и CD пересекаются в одной точке.
4. Докажите, что любой жесткий плоский треугольник T площади меньше четырёх можно просунуть сквозь треугольную дырку Q площади 3.
5. В выпуклом четырехугольнике ABCD: AC ⊥ BD, ∠BCA = 10°, ∠BDA = 20°, ∠BAC = 40°. Найдите ∠BDC.
6. Пусть AA1, BB1 и CC1 – высоты неравнобедренного остроугольного треугольника АВС; окружности, описанные около треугольников АВС и A1B1C, вторично пересекаются в точке Р, Z – точка пересечения касательных к описанной окружности треугольника АВС, проведённых в точках А и В.
Докажите, что прямые АР, ВС и ZC1 пересекаются в одной точке.
Школьная олимпиада по математике 11 класс.
1. Существуют ли два таких четырехугольника, что стороны первого меньше соответствующих сторон второго, а соответствующие диагонали больше?
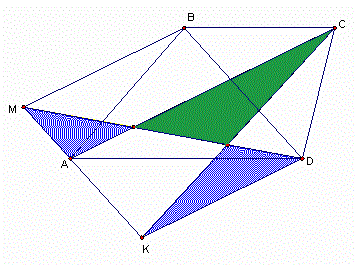
2. Трапеция ABCD и параллелограмм MBDK расположены так, что стороны параллелограмма параллельны диагоналям трапеции (см. рис.). Докажите, что площадь зеленой части равна сумме площадей синих частей.
3. В остроугольном треугольнике АВС проведены высоты АА1 и ВВ1.
Докажите, что перпендикуляр, опущенный из точки касания вписанной окружности со стороной ВС на прямую АС, проходит через центр вписанной окружности треугольника А1СВ1.
4. На медианах треугольника как на диаметрах построены три окружности. Известно, что они попарно пересекаются. Пусть C1 — более удаленная от вершины C точка пересечения окружностей, построенных на медианах AM1 и BM2. Точки A1 и B1 определяются аналогично. Докажите, что прямые АА1, ВВ1 и СС1 пересекаются в одной точке.
5. Докажите, что у любого выпуклого многогранника найдутся три ребра, из которых можно составить треугольник.
6. К двум окружностям w1 и w2, пересекающимся в точках А и В, проведена их общая касательная CD
(C и D — точки касания соответственно, точка B ближе к прямой CD, чем А).
Прямая, проходящая через А, вторично пересекает w1 и w2 в точках К и L соответственно (A лежит между K и L).
Прямые KC и LD пересекаются в точке p.
Докажите, что РВ — симедиана треугольника KpL (прямая, симметричная медиане относительно биссектрисы).


