ЕГЭ 2022 по математике задание 14 с решением

Демонстрационный вариант ЕГЭ 2022 по математике
ЕГЭ по математике 2022 в формате pdf Базовый уровень | Профильный уровень
Задания для подготовки к ЕГЭ по математике: базовый и профильный уровень с ответами и решением.
Математика: базовый | профильный 1-12 | 13 | 14 | 15 | 16 | 17 |
18 | 19 | Главная
ЕГЭ 2022 по математике задание 14
ЕГЭ 2022 по математике профильный уровень задание 14 с решением
ЕГЭ 2022 по математике задание 14
Решите:
Ребро куба равно корень из 6.
Найдите расстояние между диагональю куба и диагональю любой из его граней.
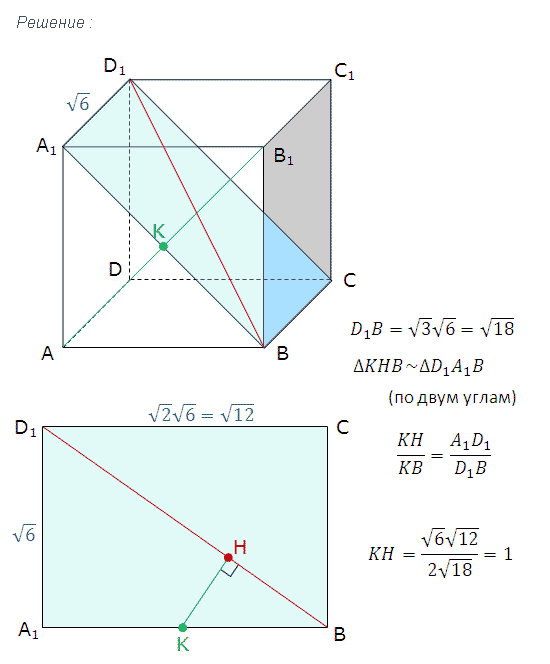
ЕГЭ 2022 по математике задание 14
В правильной треугольной пирамиде АВСS с основанием АВС известны ребра: АВ= 5 корней из 3, SC= 13.
Найти угол, образованный плоскостью основания и прямой, проходящей через середину ребер АS и ВС.
Решение:
1. Поскольку SABC - правильная пирамида, то ABC - равносторонний треугольник, а остальные грани - равные между собой равнобедренные треугольники.
То есть все стороны основания равны 5 sqrt(3), а все боковые ребра равны 13.
2. Пусть D - середина BC, E - середина AS, SH - высота, опущенная из точки S к основанию пирамиды, EP - высота, опущенная из точки E к основанию пирамиды.
3. Найдем AD из прямоугольного треугольника CAD по теореме Пифагора. Получится 15/2 = 7.5.
4. Поскольку пирамида правильная, точка H - это точка пересечения высот/медиан/биссектрис треугольника ABC, а значит, делит AD в отношении 2:1 (AH=2 AD).
5. Найдем SH из прямоугольного треугольника ASH. AH=AD 2/3 = 5, AS = 13, по теореме Пифагора SH = sqrt(132-52) = 12.
6. Треугольники AEP и ASH оба прямоугольные и имеют общий угол A, следовательно, подобные. По условию, AE = AS/2, значит, и AP = AH/2, и EP = SH/2.
7. Осталось рассмотреть прямоугольный треугольник EDP (нас как раз интересует угол EDP).
EP = SH/2 = 6;
DP = AD 2/3 = 5;
Тангенс угла EDP = EP/DP = 6/5,
Угол EDP = arctg(6/5)
Ответ: arctg(6/5)
|
Еще задания 14 профильного уровня егэ по математике с решением



