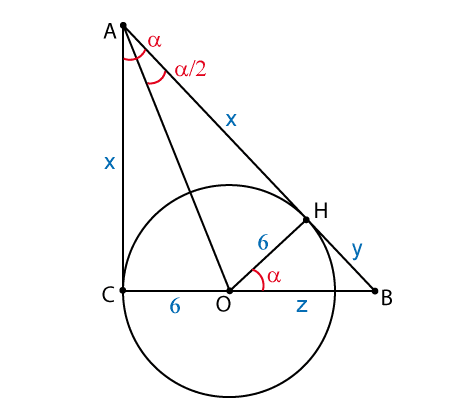ЕГЭ 2022 по математике задание 16
Условие:
Прямоугольный треугольник ABC имеет периметр 54.
Окружность радиуса 6, центр которой лежит на катете ВС, касается прямых АВ и АС.
Найти площадь треугольника АВС.
Решение:
Пусть AC = AH = x, BH = y, BO = z.
Тогда периметр треугольника равен 2x+y+z+6 = 54.
Выразим x, y и z через угол альфа (а):
Из прямоугольного треугольника AHO:
x = 6/tg(a/2).
Из прямоугольного треугольника BHO:
y = 6 tg(a), z = 6/cos(a)
Итак, выражение для периметра становится таким:
12/tg(a/2)+6 tg(a)+6/cos(a)+6 = 54
1/cos(a) + 2/tg(a/2) + tg(a) = 8.
Тут удобно всё выразить через тангенс половинного угла:
(1+(tg(a/2))
2)/(1-(tg(a/2))
2) + 2/tg(a/2) + 2 tg(a/2)/(1-(tg(a/2))
2) = 8.
Обозначим t = tg(a/2), получим
(1+t
2)/(1-t
2)+2/t+2t/(1-t
2) = 8
Путём несложных преобразований приводим это к виду
9t
2 - 9t + 2 = 0
(1) t1 = 1/3
(2) t2 = 2/3
Выражаем обратно x и z (y нам в принципе уже не нужен, поскольку площадь треугольника будет равна половине произведения катетов, т.е. x (z+6)/2. Хотя и y тоже по хорошему стоит вычислить и проверить, получается ли периметр равным 54).
Итак, для случая (1) имеем:
z = 6/cos(a) = 6/((1-1/9)/(1+1/9)) = 7.5
x = 6/tg(a/2) = 6/(1/3) = 18.
S = x (z+6)/2 = 121.5
Для случая (2) имеем:
z = 6/cos(a) = 6/((1-4/9)/(1+4/9)) = 15.6
x = 6/tg(a/2) = 6/(2/3) = 9.
S = x (z+6)/2 = 97.2
Ответ:
121.5, 97.2
ЕГЭ 2022 по математике задание 16
Окружность S проходит через вершину C прямого угла и пересекает его стороны в точках, удаленных от вершины C на расстояние 14 и 48. Найти радиус окружности, вписанной в данный угол и касающейся окружности S.
Решение:
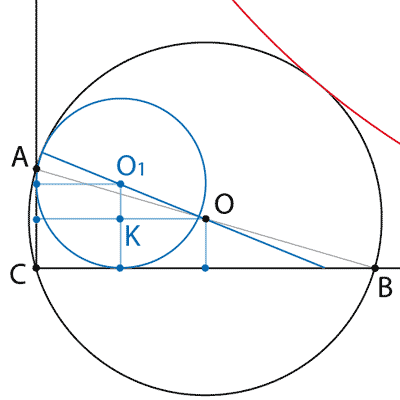
Во-первых, заметим, что, как и обычно бывает в C4, тут может быть два случая - вторая окружность может касаться первой как изнутри (синие линии на рисунке), так и снаружи (красная линия).
Итак, AC = 14, BC = 48, угол C - прямой. Значит, AB является диаметром первой окружности, и он равен sqrt(14
2+48
2) = 50.
Точка O, являясь центром окружности, делит AB пополам. Значит, перпендикуляры, опущенные из неё к отрезкам AC и BC, тоже делят их пополам.
Пусть O1 - центр второй окружности, а R - её радиус. Рассмотрим прямоугольный треугольник OKO1 с гипотенузой OO1 и катетами, параллельными лучам угла.
В "синем" случае:
OK = 24 - R
O1K = R - 7
OO1 = 25 - R
Пишем теорему Пифагора:
(24 - R)
2 + (R - 7)
2 = (25 - R)
2 Решаем, получаем два корня - 0 и 12. Нулевой случай нас не сильно интересует.
В "красном" случае всё то же самое, только OK = R - 24 и, что самое важное, OO1 = 25 + R.
И там, решая такое же уравнение, получим второй корень 112.
Ответ: 12, 112
|
Еще задания 16 профильного уровня егэ по математике с решением