ЕГЭ по математике
Условие:
Найдите все положительные значения параметра а,
при каждом из которых уравнение аx = x имеет единственное решение.
Решение:
Пусть f(x) = ax, g(x) = x.
Функция g(x) - непрерывная, строго возрастающая на всей области определения и может принимать любое значение от минус бесконечности до плюс бесконечности.
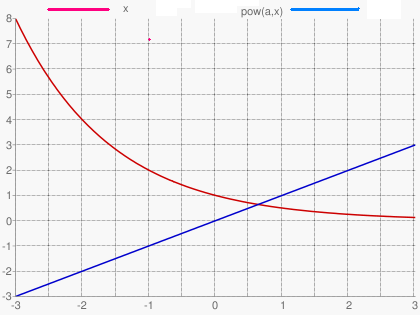
При 0 < a < 1 функция f(x) - непрерывная, строго убывающая на всей области определения и может принимать значения в интервале (0;+бесконечность). Поэтому при любых таких a уравнение f(x) = g(x) имеет ровно одно решение.
При a = 1 функция f(x) тождественно равна единице, и уравнение f(x) = g(x) также имеет единственное решение x = 1.
При a > 1:
Производная функции h(x) = (a
x - x) равна
(a
x - x) = a
x ln(a) - 1
Приравняем её к нулю:
a
x ln(a) = 1
a
x = 1/ln(a)
x = -log_a(ln(a)).
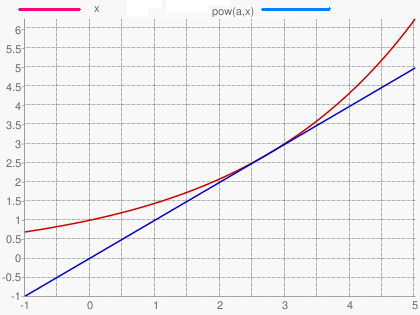
У производной единственный ноль. Слева от этого значения функция h(x) убывает, справа - возрастает.
Поэтому она либо вообще не имеет нулей, либо имеет два нуля. И один корень она имеет только в том случае, когда он совпадает с найденным экстремумом.
То есть, нам требуется найти такое значение a, при котором функция
h(x) = a
x - x достигает экстремума и обращается в ноль в одной и той же точке. Иными словами, когда прямая y = x является касательной к графику функции a
x.
То есть
a
x = x
a
x ln(a) = 1
Подставляем a
x = x во второе уравнение:
x ln(a) = 1, откуда ln(a) = 1/x, a = e
(1/x).
Снова подставляем во второе уравнение:
(e
(1/x))
x (1/x) = 1
e
1 = x
x = e.
А это подставляем в первое уравнение:
a
e = e
a = e
(1/e) Ответ:
(0;1]{e
(1/e)}
ЕГЭ по математике
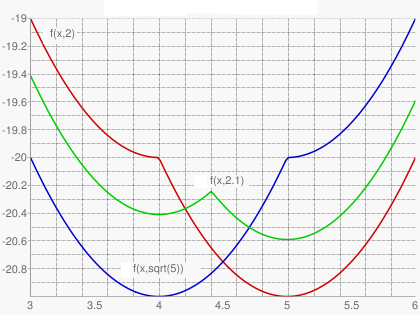
Найти все значения параметра a, при которых функция
f(x) = x
2 - |x-a
2| - 9x
имеет хотя бы одну точку максимума.
Решение: Раскроем модуль:
При x <= a
2: f(x) = x
2 - 8x - a
2,
при x > a
2: f(x) = x
2 - 10x + a
2.
Производная левой части: f'(x) = 2x - 8
Производная правой части: f'(x) = 2x - 10
И левая, и правая части могут иметь только минимум. Значит, единственный максимум у функции f(x) может быть в том и только в том случае, если в точке x=a
2 левая часть возрастает (то есть 2x-8 > 0), а правая — убывает (то есть 2x-10 < 0).
То есть, получаем систему:
2x-8 > 0
2x-10 < 0
x = a
2 откуда
4 < a
2 < 5
a ~ (-sqrt(5); -2) ~ (2; sqrt(5))
Ответ: (-sqrt(5); -2) ~ (2; sqrt(5))
|
Еще задания 18 профильного уровня егэ по математике с решением